The yearly GATE exam is right around the corner. For some this was a long time coming—for others, a last minute priority. Whichever group you belong to, preparation would be the only focus for you now.
This article is here to assist with those efforts. A curated list of GATE DA learning material that would get you the right topics required for overcoming the exam.
The learning is supplemented with questions that put to test your standing and proficiency in the exam.
GATE DA: Decoded
GATE DA is the Data Science and Artificial Intelligence paper in the GATE exam that tests mathematics, programming, data science, machine learning, and AI fundamentals. Here’s the syllabus for the paper:
GATE DA Syllabus: https://gate2026.iitg.ac.in/doc/GATE2026_Syllabus/DA_2026_Syllabus.pdf
To summarize, the paper consists of the following subjects:
- Probability and Statistics
- Linear Algebra
- Calculus and Optimization
- Machine Learning
- Artificial Intelligence
If you’re looking for resources on a specific subject, just click on one of the above links to get to the required section.
1. Probability and Statistics

Probability and Statistics builds the foundation for reasoning under uncertainty, helping you model randomness, analyze data, and draw reliable inferences from samples using probability laws and statistical tests.
Articles:
- Statistics and Probability: This sets the mental model. What is randomness? What does a sample represent? Why do averages stabilize? Read this to orient yourself before touching equations.
- Basics of Probability: This is where intuition meets rules. Conditional probability, independence, and Bayes are introduced in a way that mirrors how they appear in exam questions.
- Introduction to Probability Distributions: Once probabilities make sense, distributions explain how data behaves at scale.
Video learning: If you prefer a guided walkthrough or want to reinforce concepts visually, use the following YouTube playlist: Probability and Statistics
Questions (click to expand)
Q1. Two events A and B are independent. Which statement is always true?
Click here to view the answer
Correct option: P(A ∩ B) = P(A)P(B)
Independence means the joint probability equals the product of marginals.
Q2. Which distribution is best suited for modeling the number of arrivals per unit time?
Click here to view the answer
Correct option: Poisson
Poisson models counts of independent events in a fixed interval (time/space).
Q3. If X and Y are uncorrelated, then:
Click here to view the answer
Correct option: Cov(X, Y) = 0
Uncorrelated means covariance is zero. Independence is stronger and doesn’t automatically follow.
Q4. Which theorem explains why sample means tend to be normally distributed?
Click here to view the answer
Correct option: Central Limit Theorem
The CLT says the distribution of sample means approaches normal as sample size increases (under broad conditions).
If you can reason about uncertainty and variability, the next step is learning how data and models are represented mathematically, which is where linear algebra comes in.
2. Linear Algebra
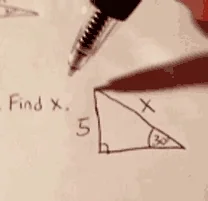
Linear Algebra provides the mathematical language for data representation and transformation, forming the core of machine learning models through vectors, matrices, and decompositions.
Articles:
- Comprehensive Guide to Linear Algebra: This sets the conceptual foundation. What does a vector represent? Read this to develop geometric intuition before focusing on matrix operations.
- 12 Must Know Matrix Operations: A foundational article that goes over the fundamental operations that can be performed on a matrix. A seminal concept on which ML models are built.
- Dimensionality reduction via Single Value Distribution: This is where structure emerges. Eigenvalues, projections, and compression. These ideas directly connect to concepts on PCA, optimization, and model behavior.
Video learning: If visual intuition helps, use the following YouTube playlist to see geometric interpretations of vectors, projections, and decompositions in action: Linear Algebra
Questions (click to expand)
Q1. If a matrix A is idempotent, then:
Click here to view the answer
Correct option: A² = A
Idempotent matrices satisfy A² = A by definition.
Q2. Rank of a matrix equals:
Click here to view the answer
Correct option: Number of linearly independent rows
Rank is the dimension of the row (or column) space.
Q3. SVD of a matrix A decomposes it into:
Click here to view the answer
Correct option: A = UΣVᵀ
SVD factorizes A into orthogonal matrices U, V and a diagonal matrix Σ of singular values.
Q4. Eigenvalues of a projection matrix are:
Click here to view the answer
Correct option: Only 0 or 1
Projection matrices are idempotent (P² = P), which forces eigenvalues to be 0 or 1.
With vectors and matrices in place, the focus shifts to how models actually learn by adjusting these quantities, a process governed by calculus and optimization.
3. Calculus and Optimization

This section explains how models learn by optimizing objective functions, using derivatives and gradients to find minima and maxima that drive training and parameter updates.
Articles:
- Mathematics Behind Machine Learning: This builds intuition around derivatives, gradients, and curvature. It helps you understand what a minimum actually represents in the context of learning.
- Mathematics for Data Science: This connects calculus to algorithms. Gradient descent, convergence behavior, and second-order conditions are introduced in a way that aligns with how they appear in exam and model-training scenarios.
- Optimization Essentials: Optimization is how models improve. The essentials of optimization, from objective functions to iterative methods, and shows how these ideas drive learning in machine learning systems.
Video learning: For step-by-step visual explanations of gradients, loss surfaces, and optimization dynamics, refer to the following YouTube playlist: Calculus and Optimization
Questions (click to expand)
Q1. A necessary condition for f(x) to have a local minimum at x = a is:
Click here to view the answer
Correct option: f′(a) = 0
A local minimum must occur at a critical point where the first derivative is zero.
Q2. Taylor series is primarily used for:
Click here to view the answer
Correct option: Function approximation
Taylor series approximates a function locally using its derivatives at a point.
Q3. Gradient descent updates parameters in which direction?
Click here to view the answer
Correct option: Opposite to the gradient
The negative gradient gives the direction of steepest decrease of the objective.
Q4. If f″(x) > 0 at a critical point, the point is:
Click here to view the answer
Correct option: Minimum
Positive second derivative implies local convexity, hence a local minimum.
Once you understand how objective functions are optimized, you’re ready to see how these ideas come together in real Machine Learning algorithms that learn patterns from data.
4. Machine Learning

Machine Learning focuses on algorithms that learn patterns from data, covering supervised and unsupervised methods, model evaluation, and the trade-off between bias and variance.
Articles:
- Mathematics for Machine Learning: This builds the foundation for the algorithms used in Machine Learning.
- Machine Learning Algorithms Explained: This provides a structured overview of common supervised and unsupervised algorithms, emphasizing when and why each method is used.
- Machine Learning Life Cycle Explained: This ties everything together. Data preparation, training, validation, bias–variance trade-off, and model evaluation are discussed as a single pipeline rather than isolated steps.
Video learning: To reinforce concepts like overfitting, regularization, and distance-based learning, use the following YouTube playlist: Machine Learning
Questions (click to expand)
Q1. Which algorithm is most sensitive to feature scaling?
Click here to view the answer
Correct option: K-Nearest Neighbors
KNN uses distances, so changing feature scales changes the distances and neighbors.
Q2. Ridge regression primarily addresses:
Click here to view the answer
Correct option: Multicollinearity
L2 regularization stabilizes coefficients when predictors are correlated.
Q3. PCA reduces dimensionality by:
Click here to view the answer
Correct option: Maximizing variance
Principal components capture directions of maximum variance in the data.
Q4. Bias-variance trade-off refers to:
Click here to view the answer
Correct option: Underfitting vs overfitting
Higher model complexity tends to reduce bias but increase variance.
Having seen how models are trained and evaluated, the final step is understanding how Artificial Intelligence systems reason, search, and make decisions under uncertainty.
5. Artificial Intelligence

Artificial Intelligence deals with decision-making and reasoning, including search, logic, and probabilistic inference, enabling systems to act intelligently under uncertainty.
Articles:
- Introduction to Artificial Intelligence for Beginners: This sets the big picture. Search strategies, problem formulation, and intelligent agents are introduced to frame how AI systems operate.
- How Does Artificial Intelligence Work?: This dives into uncertainty-aware decision-making. Bayesian networks, conditional independence, and inference algorithms are central to many AI questions in GATE.
- AI Interview Questions: This would serve as a checklist of commonly asked questions on AI. This will cover the breadth of the domain.
Video learning: For visual walkthroughs of search algorithms, game-playing strategies, and inference methods, use the following YouTube playlist: Artificial Intelligence
Questions (click to expand)
Q1. BFS is preferred over DFS when:
Click here to view the answer
Correct option: Shortest path is required
BFS guarantees the shortest path in unweighted graphs.
Q2. Minimax algorithm is used in:
Click here to view the answer
Correct option: Adversarial search
Minimax models optimal play in two-player zero-sum games.
Q3. Conditional independence is crucial for:
Click here to view the answer
Correct option: Naive Bayes
Naive Bayes assumes features are conditionally independent given the class.
Q4. Variable elimination is an example of:
Click here to view the answer
Correct option: Exact inference
Variable elimination computes exact marginals in probabilistic graphical models.
More help
To tell whether you are prepared on the subject, the questions would serve as a litmus test. If you struggled to get through the questions, then more learning is required. Here are all the YouTube playlists subject wise:
- Probability and Statistics
- Linear Algebra
- Calculus and Optimization
- Machine Learning
- Artificial Intelligence
If this learning material is too much for you, then you might consider short form content covering Artificial Intelligence and Data Science.
If you were unable to find the resources helpful, then checkout the GitHub repository on GATE DA. Curated by aspirants who had cracked the exam, the repo is a treasure trove of content for data science and artificial intelligence.
With the resources and the questions out of the way, the only thing left is for you to decide how you’re gonna approach the learning.





