Introduction
Understanding the shape of data is crucial while practicing data science. It helps to understand where the most information lies and analyze the outliers in a given data. In this article, we’ll learn about the shape of data, the importance of skewness, and kurtosis in statistics. The types of skew and kurtosis , Analyze the shape of data in the given dataset. Let’s first understand what skewness and kurtosis is. In this article you will clear your doubts about the kurtosis and skewness. With that you will also get to know about the skewness and kurtosis interpretation and what is kurtosis in statistics or kurtosis in skewness so on all of these you will get to learn and at the end of this article you will clear your all doubts.
“Skewness essentially is a commonly used measure in descriptive statistics that characterizes the asymmetry of a data distribution, while kurtosis determines the heaviness of the distribution tails.”
Learning Objectives
- In this article, you will learn about Skewness and its different types.
- You will learn how to calculate the Skewness Coefficient.
- This article will also help you learn about Kurtosis and its type.
Table of contents
What is Skewness?
Skewness is a statistical measure that assesses the asymmetry of a probability distribution. It quantifies the extent to which the data is skewed or shifted to one side.
Positive skewness indicates a longer tail on the right side of the distribution, while negative skewness indicates a longer tail on the left side. Skewness helps in understanding the shape and outliers in a dataset.
Depending on the model, skewness in the values of a specific independent variable (feature) may violate model assumptions or diminish the interpretation of feature importance.
A probability distribution that deviates from the symmetrical normal distribution (bell curve) in a given set of data exhibits skewness, which is a measure of asymmetry in statistics.
A skewed data set, typical values fall between the first quartile (Q1) and the third quartile (Q3).
The normal distribution helps to know a skewness. When we talk about normal distribution, data symmetrically distributed. The symmetrical distribution has zero skewness as all measures of a central tendency lies in the middle.
In a symmetrically distributed dataset, both the left-hand side and the right-hand side have an equal number of observations. (If the dataset has 90 values, then the left-hand side has 45 observations, and the right-hand side has 45 observations.). But, what if not symmetrical distributed? That data is called asymmetrical data, and that time skewness comes into the picture.
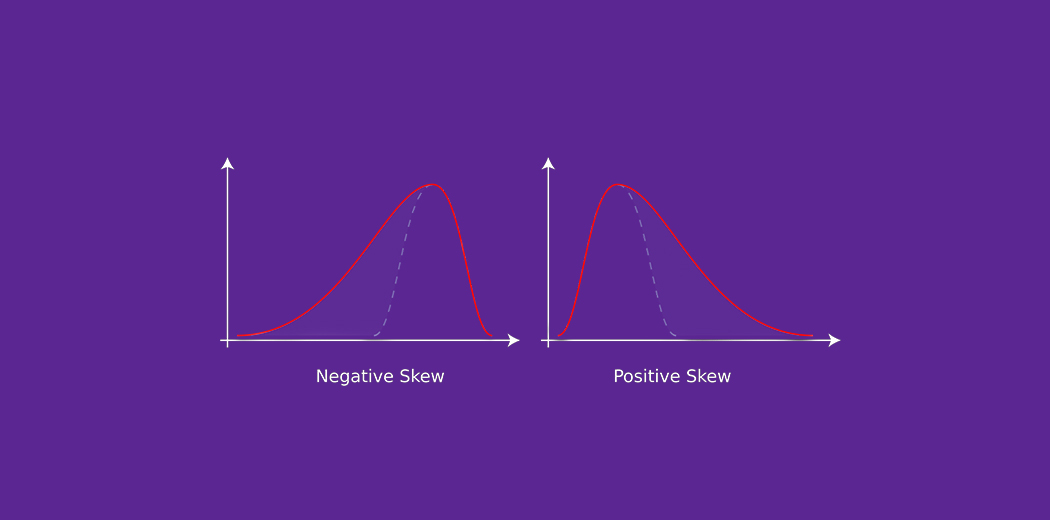
Types of Skewness
Positive Skewed or Right-Skewed (Positive Skewness)
In statistics, a positively skewed or right-skewed distribution has a long right tail. It is a sort of distribution where the measures are dispersing, unlike symmetrically distributed data where all measures of the central tendency (mean, median, and mode) equal each other. This makes Positively Skewed Distribution a type of distribution where the mean, median, and mode of the distribution are positive rather than negative or zero.
In positively skewed, the mean of the data is greater than the median (a large number of data-pushed on the right-hand side). In other words, the results are bent towards the lower side. The mean will be more than the median as the median is the middle value and mode is always the most frequent value.
Extreme positive skewness is not desirable for a distribution, as a high level of skewness can cause misleading results. The data transformation tools are helping to make the skewed data closer to a normal distribution. For positively skewed distributions, the famous transformation is the log transformation. The log transformation proposes the calculations of the natural logarithm for each value in the dataset.
Negative Skewed or Left-Skewed (Negative Skewness)
A distribution with a long left tail, known as negatively skewed or left-skewed, stands in complete contrast to a positively skewed distribution. skewness and kurtosis in statistics, negatively skewed distribution refers to the distribution model where more values are plots on the right side of the graph, and the tail of the distribution is spreading on the left side.
In negatively skewed, the mean of the data is less than the median (a large number of data-pushed on the left-hand side). Negatively Skewed Distribution is a type of distribution where the mean, median, and mode of the distribution are negative rather than positive or zero.
Median is the middle value, and mode is the most frequent value. Due to an unbalanced distribution, the median will be higher than the mean.
How to Calculate the Skewness Coefficient?
Various methods can calculate skewness, with Pearson’s coefficient being the most commonly used method.
Pearson’s first coefficient of skewness
To calculate skewness values, subtract the mode from the mean, and then divide the difference by standard deviation.
As Pearson’s correlation coefficient differs from -1 (perfect negative linear relationship) to +1 (perfect positive linear relationship), including a value of 0 indicating no linear relationship, When we divide the covariance values by the standard deviation, it truly scales the value down to a limited range of -1 to +1. That accurately shows the range of the correlation values.
Pearson’s first coefficient of skewness is helping if the data present high mode. However, if the data exhibits low mode or multiple modes, it is preferable not to use Pearson’s first coefficient, and instead, Pearson’s second coefficient may be superior, as it does not depend on the mode.
Pearson’s second coefficient of skewness
subtract the median from the mean, multiply the difference by 3, and divide the product by the standard deviation.
Rule of thumb:
- For skewness values between -0.5 and 0.5, the data exhibit approximate symmetry.
- Skewness values within the range of -1 and -0.5 (negative skewed) or 0.5 and 1(positive skewed) indicate slightly skewed data distributions.
- Data with skewness values less than -1 (negative skewed) or greater than 1 (positive skewed) are considered highly skewed.
What is Kurtosis?
Kurtosis is a statistical measure that quantifies the shape of a probability distribution. It provides information about the tails and peakedness of the distribution compared to a normal distribution.
Positive kurtosis indicates heavier tails and a more peaked distribution, while negative kurtosis suggests lighter tails and a flatter distribution. Kurtosis helps in analyzing the characteristics and outliers of a dataset.
The measure of Kurtosis refers to the tailedness of a distribution. Tailedness refers to how often the outliers occur.
Peakedness in a data distribution is the degree to which data values are concentrated around the mean. Datasets with high kurtosis tend to have a distinct peak near the mean, decline rapidly, and have heavy tails. Datasets with low kurtosis tend to have a flat top near the mean rather than a sharp peak.
In finance, kurtosis is used as a measure of financial risk. A large kurtosis is associated with a high level of risk for an investment because it indicates that there are high probabilities of extremely large and extremely small returns. On the other hand, a small kurtosis signals a moderate level of risk because the probabilities of extreme returns are relatively low.
What is Excess Kurtosis?
In statistics and probability theory, researchers use excess kurtosis to compare the kurtosis coefficient with that of a normal distribution. Excess kurtosis can be positive (Leptokurtic distribution), negative (Platykurtic distribution), or near zero (Mesokurtic distribution). Since normal distributions have a kurtosis of 3, excess kurtosis is calculated by subtracting kurtosis by 3.
Excess kurtosis = Kurt – 3
Types of Kurtosis
Kurtosis is a statistical measure that describes the shape of a probability distribution’s tails relative to its peak. There are three main types of kurtosis:
- Mesokurtic: A distribution with mesokurtic kurtosis has a similar peak and tail shape as the normal distribution. It has a kurtosis value of around 0, indicating that its tails are neither too heavy nor too light compared to a normal distribution.
- Leptokurtic: A distribution with leptokurtic kurtosis has heavier tails and a sharper peak than the normal distribution. It has a positive kurtosis value, indicating that it has more extreme outliers than a normal distribution. This type of distribution is often associated with higher peakedness and a greater probability of extreme values.
- Platykurtic: A distribution with platykurtic kurtosis has lighter tails and a flatter peak than the normal distribution. It has a negative kurtosis value, indicating that it has fewer extreme outliers than a normal distribution. This type of distribution is often associated with less peakedness and a lower probability of extreme values.
Skewness and Kurtosis Formula
Skewness and kurtosis are two statistical measures that describe the shape of a distribution. Let’s look at skewness and kurtosis formula in the next section!
Skewness Formula
Skewness measures the asymmetry of a distribution. A symmetrical distribution has a skewness of zero. Positive skewness indicates that the right tail of the distribution is longer or fatter than the left tail, while negative skewness indicates the opposite.
The formula for skewness (often denoted by 𝛾1γ1) for a sample is:
γ1=(n−1)(n−2)n∑i=1n(sxi−xˉ)3
Where:
- 𝑛n is the number of observations in the sample
- 𝑥𝑖xi is the ith observation
- 𝑥ˉxˉ is the sample mean
- 𝑠s is the sample standard deviation
Kurtosis Formula
Kurtosis measures the peakedness or flatness of a distribution relative to the normal distribution. A normal distribution has a kurtosis of 3, known as the excess kurtosis. Deviations from this value indicate how much the distribution deviates from the normal, with positive excess kurtosis indicating a more peaked distribution and negative excess kurtosis indicating a flatter one.
The formula for kurtosis (often denoted by 𝛾2γ2) for a sample is:
γ2=(n−1)(n−2)(n−3)n(n+1)∑i=1n(sxi−xˉ)4−(n−2)(n−3)3(n−1)2
Where:
- 𝑛n is the number of observations in the sample
- 𝑥𝑖xi is the ith observation
- 𝑥ˉxˉ is the sample mean
- 𝑠s is the sample standard deviation
These formulas give the sample skewness and kurtosis. For population skewness and kurtosis, the divisor 𝑛n in the formulas is replaced with 𝑛−1n−1 and 𝑛−2n−2, respectively.
Difference Between Skewness and Kurtosis
| Skewness | Kurtosis |
|---|---|
| Skewness measures the asymmetry of a probability distribution | Kurtosis measures the tailedness or peakedness of a probability distribution |
| Positive skew indicates a right-skewed distribution, with the tail extending to the right | Positive kurtosis indicates a distribution with heavier tails, often referred to as “leptokurtic” |
| Negative skew indicates a left-skewed distribution, with the tail extending to the left | Negative kurtosis indicates a distribution with lighter tails, often referred to as “platykurtic” |
| A skewness value of zero indicates a symmetric distribution | A kurtosis value of zero indicates a distribution similar to the normal distribution, often referred to as “mesokurtic” |
| Used to identify the direction and degree of asymmetry | Used to identify the presence of outliers or extreme values |
| Sensitive to changes in the tails of the distribution | Sensitive to changes in the center and shoulders of the distribution |
| Commonly used in fields such as economics, finance, and social sciences | Commonly used in statistics, engineering, and physical sciences |
| Examples: income distribution, stock returns | Examples: particle physics, image processing |
Conclusion
Skewness and Kurtosis naturally complement each other in analyzing data distributions. Skewness, which measures the symmetry or asymmetry of data distribution, helps us understand if the data is pushed towards one side or the other. For instance, positive skewness indicates a distribution pushed towards the right side, while negative skewness implies a distribution pushed towards the left side. On the other hand, Kurtosis helps determine whether the data exhibits a heavy-tailed or light-tailed distribution. By incorporating both Skewness and Kurtosis into our analysis, we gain a more comprehensive understanding of the shape and characteristics of the data.
Skewness indicates the degree of tilt in data, whether it leans towards the left or right, exposing any asymmetry present. A positive skew indicates a tail extending towards the right, whereas a negative skew leans in the opposite direction.
Kurtosis, on the other hand, focuses on the distribution’s peaks and tails.
Skewed data may cause the tail region to act as an outlier for the statistical model, and such outliers can adversely impact the performance of the model, particularly in regression-based models. Some statistical models are robust to outliers like Tree-based models, but it will limit the possibility of trying other models. So there is a necessity to transform the skewed data to be close enough to a Normal distribution.
Hope you like the article and get understanding about the skewness and kurtosis in statistics,skewness and kurtosis interpretation and also about the kurtosis in statistics with that you will know the difference b/w skewness and kurtosis and it will help you in to make report.
Key Takeaways
- Skewness is a statistical measure of the asymmetry of a probability distribution. It characterizes the extent to which the distribution of a set of values deviates from a normal distribution.
- Skewness between -0.5 and 0.5 is symmetrical.
- Kurtosis determines whether the data exhibits a heavy-tailed or light-tailed distribution.
- Data sets with high kurtosis have heavy tails and more outliers, while data sets with low kurtosis tend to have light tails and fewer outliers.
- Excess kurtosis can be positive (Leptokurtic distribution), negative (Platykurtic distribution), or near zero (Mesokurtic distribution).
- With these Skewness and Kurtosis interpretation, you will understand the concept of kurtosis in statistics and kurtosis in skewness to how its measure the shape of this probality distribution.
Frequently Asked Questions
Q1. Is kurtosis a measure of shape?
A. Kurtosis describes the shape of the distribution tale in relation to its overall shape. Low kurtosis can sharply peak a distribution, while high kurtosis can result in a distribution with a lower peak.
Q2. What do you mean by kurtosis?
A. Kurtosis assesses how pointy and heavy-tailed a distribution is.
Skewness quantifies the lack of symmetry in a distribution.
Q3. What is the shape of a data distribution?
A. A distribution of data item values may be symmetrical or asymmetrical. Two common examples of symmetry and asymmetry are the ‘normal distribution’ and the ‘skewed distribution.’
Q4. What is a good skewness and kurtosis value?
An ideal skewness value is approximately 0, suggesting a balanced distribution. A kurtosis value close to 3 represents a distribution that is considered normal.
Q5. How to report skewness and kurtosis?
Skewness:
Positive skewness: Right-skewed (longer right tail).
Negative skewness: Left-skewed (longer left tail).
Report skewness value with direction (positive/negative) and magnitude (low/moderate/high).
Kurtosis:
Excess kurtosis (compared to normal distribution):Kurtosis = 3: Similar to normal distribution.
Kurtosis > 3: Leptokurtic (sharper peak, more outliers).
Kurtosis < 3: Platykurtic (flatter peak, fewer outliers).
Report kurtosis value with comparison to normal distribution and brief interpretation (lepto/platy).
The media shown in this article on skewness and Kurtosis are not owned by Analytics Vidhya and is used at the Author’s discretion.
blogathonexplain skewness and kurtosisformula for skewness and kurtosisKurtosiskurtosis and skewnesskurtosis in statisticsskew and kurtosisSkewnessskewness and kurtosisskewness and kurtosis formulaskewness and kurtosis in statisticsskewness and kurtosis interpretationwhat is kurtosis and skewnesswhat is skewness and kurtosis
Hi SUVARNA3, I am a data scientist at KNIME and I really like your article! How can I get in touch with you?
yes l am intersting for you lesson today.
thanks , keep it up
Hii Roberto, you can connect with me over mail: [email protected] Thank you
Very clear, Thanks a lot.