Descriptive statistics | A Beginners Guide!

Descriptive Statistics

1. Central Tendency of Data

1.1 Mean

1.2 Median

1.3 Mode

2. Dispersion of Data

2.1 Inter Quartile Range ( IQR )

2.2 Range

2.3 Standard Deviation

2.4 Variance

3. Shape of the Data

3.1 Symmetric

3.2 Skewness

3.3 Kurtosis

Diving into the topics,

Once we have collected the data, what will we do with it? Data can be analyzed and used in various methods and formats. There are two types of statistical methods widely used for analyzing data.

1. Descriptive statistics
2. Inferential statistics

While analyzing a dataset, We use statistical methods to arrive at a conclusion. Data-driven decision-making also depends on how efficiently we use these methods.

Now, let us dive into these methods deeply.

1. Descriptive statistics

The study of numerical and graphical ways to describe and display your data is called descriptive statistics. It describes the data and helps us understand the features of the data by summarizing the given sample set or population of data. In descriptive statistics, we usually take the sample into account.

https://pixabay.com/illustrations/presentation-statistic-boy-1454403/

We can describe these data in various dimensions. Various dimensions of describing data are

1. Central Tendency of Data

2. Dispersion of Data

3. Shape of the Data

1. Central Tendency Of Data

This is the center of the distribution of data. It describes the location of data and concentrates where the data is located.

The three most widely used measures of the “center” of the data are

1.1 Mean

1.2 Median

1.3 Mode

Let us see these measures in detail,

1.1 Mean

The “Mean” is the average of the data.

Average can be identified by summing up all the numbers and then dividing them by the number of observation.

Mean = X₁ + X₂ + X₃ +… +  X_n / n

Example: 

Data – 10,20,30,40,50  and Number of observations = 5

Mean = [ 10+20+30+40+50 ] / 5

Mean = 30

Outliers influence the central tendency of the data.

What are Outliers?
Outliers are extreme behaviours. An outlier is a data point that differs significantly from other observations. It can cause serious problems in analysis.

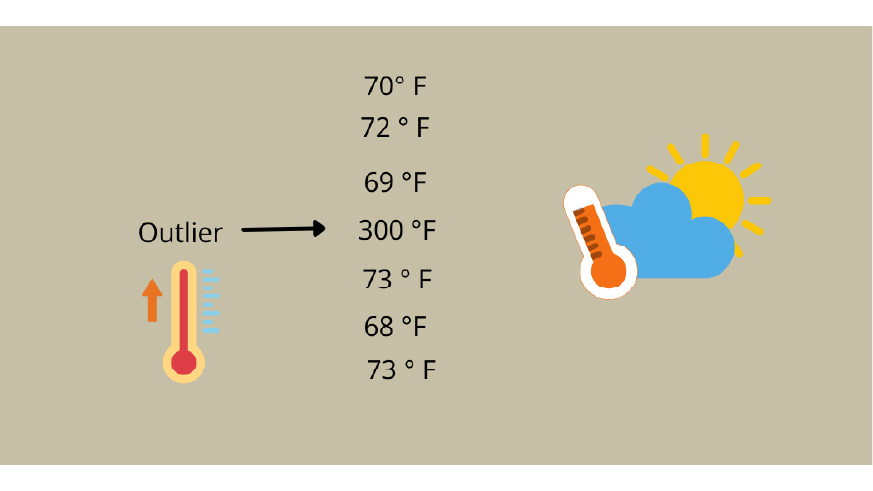
Example :

Data – 10,20,30,40,200

Mean = [ 10+20+30+40+200 ] / 5

Mean = 60

Solution for Outliers problem

Removing the outliers while taking average will give us good results.

1.2 Median

Median is the 50%^th percentile of the data. It is exactly the center point of the data.

Median can be identified by ordering the data and splits the data into two equal parts and find the number. It is the best way to find the center of the data.

Because the central tendency of the data is not affected by outliers. Outliers don’t influence the data.

Example:

Odd number of Data – 10,20,30,40,50

Median is 30.

Even number of data – 10,20,30,40,50,60

Find the middle 2 data and take the mean of that two values.

Here 30 and 40 are middle values.

30+40 / 2  =35

 Median is 35

1.3 Mode

Mode is frequently occurring data or elements.

If an element occurs the highest number of times, it is the mode of that data. If no number in the data is repeated, then there is no mode for that data. There can be more than one mode in a dataset if two values have the same frequency and also the highest frequency.

Outliers don’t influence the data.

The mode can be calculated for both quantitative and qualitative data.

Example

Data – 1,3,4,6,7,3,3,5,10, 3

Mode is 3

because 3 has the highest frequency ( 4 times)

2. Dispersion of Data

 

The dispersion is the “Spread of the data”. It measures how far the data is spread.

In most of the dataset, the data values are closely located near the mean. On some other dataset, the values are widely spread out of the mean. These dispersions of data can be measured by 

2.1 Inter Quartile Range ( IQR )

2.2 Range

2.3 Standard Deviation

2.4 Variance

Let us see these measures in detail,

1. Inter Quartile Range ( IQR )

Quartiles are special percentiles.

1st Quartile Q1 is the same as the 25th percentile.

2nd Quartile Q2 is the same as 50th percentile.

3rd Quratile Q3 is same as 75th percentile

Steps to find quartile and percentile

–The data should sorted and ordered from the smallest to the largest.

–For Quartiles, ordered data is divided into 4 equal parts.

–For Percentiles, ordered data is divided into 100 equal parts.

Inter Quartile Range is the difference between the third quartile(Q3) and the first Quartile (Q1)

IQR = Q3- Q1

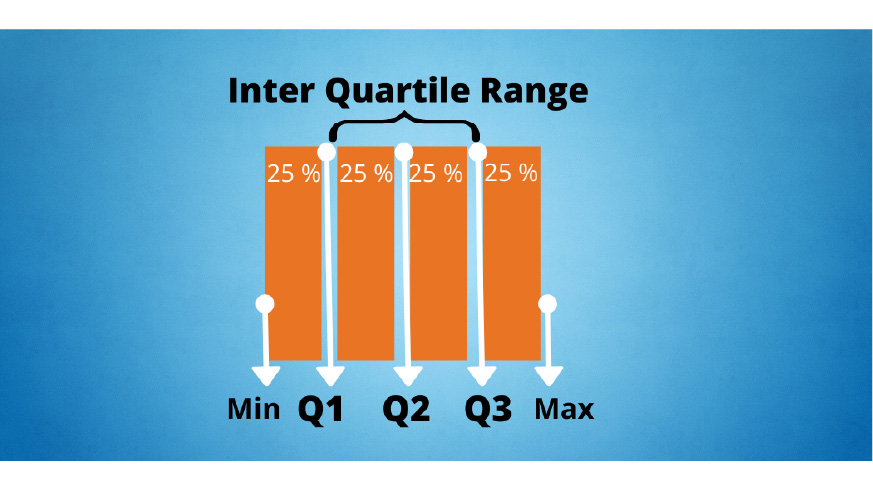
Inter Quartile range

It is the spread of the middle half(50%) of the data

2.2 Range

The range is the difference between the largest and the smallest value in the data.

Max – Min = Range

2.3 Standard Deviation

The most common measure of spread is the standard deviation.

The Standard deviation is the measure of how far the data deviates from the mean value.

The standard deviation formula varies for population and sample. Both formulas are similar, but not the same.

• Symbol used for Sample Standard Deviation  –  “s” (lowercase)
• Symbol used for Population Standard Deviation – “σ” (sigma, lower case)

Steps to find Standard deviation

If x is a number, then the difference “x – mean” is its deviation. The deviations are used to calculate the standard deviation.

Sample Standard Deviation, s  = Square root of sample variance 

Sample Standard Deviation, s = Square root of   [Σ(x − x ¯ )²/ n-1]   where x ¯ is average and n is  no. of samples

 

Standard Deviation for sample

Population Standard Deviation, σ = Square root of population variance

Population Standard Deviation, σ = Square root of  [ Σ(x − μ)² / N ] where μ is Mean and N is no.of population.

 

The standard deviation for population

The standard deviation is always positive or zero. It will be large when the data values are spread out from the mean.

2.4 Variance

The variance is a measure of variability. It is the average squared deviation from the mean.

The symbol σ² represents the population variance and the symbol for s² represents sample variance.

Population variance   σ² =  [ Σ(x − μ)² / N ]

Sample Variance  s²  =  [ Σ(x − x ¯ )²/ n-1 ]

3. Shape of the Data

The shape describes the type of the graph.

The shape of the data is important because making a decision about the probability of data is based on its shape.

The shape of the data can be measured by two methodologies.

3.1 Symmetric

3.2 Skewness

3.3 Kurtosis

Let us discuss in detail,

3.1 Symmetric

In the symmetric shape of the graph, the data is distributed the same on both sides.

In symmetric data, the mean and median are located close together.

The curve formed by this symmetric graph is called a normal curve.

3.2 Skewness

Skewness is the measure of the asymmetry of the distribution of data.

The data is not symmetrical (i.e) it is skewed towards one side.

Skewness is classified into two types.

1. Positive Skew

2. Negative Skew

let us see that,

1.Positively skewed

In a Positively skewed distribution, the data values are clustered around the left side of the distribution and the right side is longer.

The mean and median will be greater than the mode in the positive skew.

2.Negatively skewed

In a Negatively skewed distribution, the data values are clustered around the right side of the distribution and the left side is longer.

The mean and median will be less than the mode.

Positive.Negative skewed and unskewed

Kurtosis is the measure of describing the distribution of data.

This data is distributed in different ways. They are,

1. Platykurtic

2. Mesokurtic

3. Leptokurtic

Let us discuss in detail,

1. Platykurtic

The platykurtic shows a distribution with flat tails. Here the data is distributed faltly . The flat tails indicated the small outliers in the distribution.

2. Mesokurtic

In Mesokurtic, the data is widely distributed. It is normally distributed and it also matches normal distribution.

3. Leptokurtic

In leptokurtic, the data is very closely distributed. The height of the peak is greater than width of the peak.

Differences

To view my other blogs: Introductory statistics for data science

Endnotes

We have seen some basic descriptive stat concepts.

Thanks for reading!

I hope you enjoyed the article and increased your knowledge about Statistics. Please feel free to contact me at [email protected]   Linkedin

Want to share your thoughts? Feel free to comment below

About the author

Mohamed Illiyas

Currently, I am pursuing my Bachelor of Engineering (B.E) in Computer Science from the Government College of Engineering, Srirangam, Tamil Nadu. I am very enthusiastic about Statistics, Machine Learning, and Data Science.

Connect with me on Linkedin  Mohamed Illiyas

The media shown in this article are not owned by Analytics Vidhya and are used at the Author’s discretion.