Interview Prep
Career
GenAI
Prompt Engg
ChatGPT
LLM
Langchain
RAG
AI Agents
Machine Learning
Deep Learning
GenAI Tools
LLMOps
Python
NLP
SQL
AIML Projects

Reading list

Machine Learning Basics for a Newbie
6 Steps of Machine learning Lifecycle Introduction to Predictive Modeling
Introduction to Exploratory Data Analysis & Data Insights Descriptive Statistics Inferential Statistics How to Understand Population Distributions?
Reading Data Files into Python Different Variable Datatypes
Probability for Data Science Basic Concepts of Probability Axioms of Probability Conditional Probability
Central Tendencies for Continuous Variables Spread of Data KDE plots for Continuous Variable Overview of Distribution for Continuous variables Normal Distribution Skewed Distribution Skeweness and Kurtosis Distribution for Continuous Variable
Central Tendencies for Categorical Variables Understanding Discrete Distributions Performing EDA on Categorical Variables
Dealing with Missing Values Understanding Outliers Identifying Outliers in Data Outlier Detection in Python Outliers Detection Using IQR, Z-score, LOF and DBSCAN
Sample and Population Central Limit Theorem Confidence Interval and Margin of Error
Bivariate Analysis Introduction
Covariance Pearson Correlation Spearman's Correlation & Kendall's Tau Correlation versus Causation Tabular and Graphical methods for Bivariate Analysis Performing Bivariate Analysis on Continuous-Continuous Variables
Tabular and Graphical methods for Continuous-Categorical Variables Introduction to Hypothesis Testing P-value Two sample Z-test T-test T-test vs Z-test Performing Bivariate Analysis on Continuous-Catagorical variables
Chi-Squares Test Bivariate Analysis on Categorical Categorical Variables
Multivariate Analysis A Comprehensive Guide to Data Exploration The Data Science behind IPL
Supervised Learning vs Unsupervised Learning Reinforcement Learning Generative and Descriminative Models Parametric and Non Parametric model
Machine Learning Pipeline Preparing Dataset Build a Benchmark Model: Regression Build a Benchmark Model: Classification
Evaluation Metrics for Machine Learning Everyone should know Confusion Matrix Accuracy Precision and Recall AUC-ROC Log Loss R2 and Adjusted R2
Dealing with Missing Values Replacing Missing Values Imputing Missing Values in Data Working with Categorical Variables Working with Outliers Preprocessing Data for Model Building
Understanding Cost Function Understanding Gradient Descent Math Behind Gradient Descent Assumptions of Linear Regression Implement Linear Regression from Scratch Train Linear Regression in Python Implementing Linear Regression in R Diagnosing Residual Plots in Linear Regression Models Generalized Linear Models Introduction to Logistic Regression Odds Ratio Implementing Logistic Regression from Scratch Introduction to Scikit-learn in Python Train Logistic Regression in python Multiclass using Logistic Regression How to use Multinomial and Ordinal Logistic Regression in R ? Challenges with Linear Regression Introduction to Regularisation Implementing Regularisation Ridge Regression Lasso Regression
Introduction to K Nearest Neighbours Determining the Right Value of K in KNN Implement KNN from Scratch Implement KNN in Python
Bias Variance Tradeoff Introduction to Overfitting and Underfitting Visualizing Overfitting and Underfitting Selecting the Right Model What is Validation? Hold-Out Validation Understanding K Fold Cross Validation
Introduction to Feature Selection Feature Selection Algorithms Missing Value Ratio Low Variance Filter High Correlation Filter Backward Feature Elimination Forward Feature Selection Implement Feature Selection in Python Implement Feature Selection in R
Introduction to Decision Tree Purity in Decision Tree Terminologies Related to Decision Tree How to Select Best Split Point in Decision Tree? Chi-Squares Information Gain Reduction in Variance Optimizing Performance of Decision Tree Train Decision Tree using Scikit Learn Pruning of Decision Trees
Introduction to Feature Engineering Feature Transformation Feature Scaling Feature Engineering Frequency Encoding Automated Feature Engineering: Feature Tools
Introduction to Naive Bayes Conditional Probability and Bayes Theorem Introduction to Bayesian Adjustment Rating: The Incredible Concept Behind Online Ratings! Working of Naive Bayes Math behind Naive Bayes Types of Naive Bayes Implementation of Naive Bayes
Understanding how to solve Multiclass and Multilabled Classification Problem Evaluation Metrics: Multi Class Classification
Introduction to Ensemble Techniques Basic Ensemble Techniques Implementing Basic Ensemble Techniques Finding Optimal Weights of Ensemble Learner using Neural Network Why Ensemble Models Work well?
Introduction to Stacking Implementing Stacking Variants of Stacking Implementing Variants of Stacking Introduction to Blending Bootstrap Sampling Introduction to Random Sampling Hyper-parameters of Random Forest Implementing Random Forest Out-of-Bag (OOB) Score in the Random Forest IPL Team Win Prediction Project Using Machine Learning Introduction to Boosting Gradient Boosting Algorithm Math behind GBM Implementing GBM in python Regularized Greedy Forests Extreme Gradient Boosting Implementing XGBM in python Tuning Hyperparameters of XGBoost in Python Implement XGBM in R/H2O Adaptive Boosting Implementing Adaptive Boosing LightGBM Implementing LightGBM in Python Catboost Implementing Catboost in Python
Different Hyperparameter Tuning methods Implementing Different Hyperparameter Tuning methods GridsearchCV RandomizedsearchCV Bayesian Optimization for Hyperparameter Tuning Hyperopt
Understanding SVM Algorithm SVM Kernels In-depth Intuition and Practical Implementation SVM Kernel Tricks Kernels and Hyperparameters in SVM Implementing SVM from Scratch in Python and R
Introduction to Principal Component Analysis Steps to Perform Principal Compound Analysis Computation of Covariance Matrix Finding Eigenvectors and Eigenvalues Implementing PCA in python Visualizing PCA A Brief Introduction to Linear Discriminant Analysis Introduction to Factor Analysis
Introduction to Clustering Applications of Clustering Evaluation Metrics for Clustering Understanding K-Means Implementation of K-Means in Python Implementation of K-Means in R Choosing Right Value for K Profiling Market Segments using K-Means Clustering Hierarchical Clustering Implementation of Hierarchial Clustering DBSCAN Defining Similarity between clusters Build Better and Accurate Clusters with Gaussian Mixture Models
Understand Basics of Recommendation Engine with Case Study
8 Ways to Improve Accuracy of Machine Learning Models
Introduction to Dask Working with CuML
Introduction to Machine Learning Interpretability Framework and Interpretable Models model Agnostic Methods for Interpretability Implementing Interpretable Model Understanding SHAP Out-of-Core ML Introduction to Interpretable Machine Learning Models Model Agnostic Methods for Interpretability Game Theory & Shapley Values
Introduction to Machine Learning Interpretability Framework and Interpretable Models model Agnostic Methods for Interpretability Implementing Interpretable Model Understanding SHAP Out-of-Core ML Introduction to Interpretable Machine Learning Models Model Agnostic Methods for Interpretability Game Theory & Shapley Values
Introduction to AutoML Implementation of MLBox Introduction to PyCaret TPOT Auto-Sklearn EvalML
Pickle and Joblib Introduction to Model Deployment
Deploying Machine Learning Model using Streamlit Deploying ML Models in Docker Deploy Using Streamlit Deploy on Heroku Deploy Using Netlify Introduction to Amazon Sagemaker Setting up Amazon SageMaker Using SageMaker Endpoint to Generate Inference Deploy on Microsoft Azure Cloud Introduction to Flask for Model Deploying ML model using Flask
Model Deployment in Android Model Deployment in Iphone

Moments in Statistics – A Must Known Statistical Concept for Data Science

Chirag Goyal
Chirag Goyal Last Updated : 29 Apr, 2024
7 min read

Statistical Moments play a crucial role when we specify our probability distribution to work with since, with the help of moments, we can describe the properties of statistical distribution. Therefore, they help define the distribution. We required the statistical moments in Statistical Estimation and Testing of Hypotheses, which all are based on the numerical values arrived for each distribution. In this article, we will discuss moments in Statistics in detail.

This article was published as a part of the Data Science Blogathon. 

Table of contents

What is Moment in Statistics?

In Statistics, Moments are popularly used to describe the characteristic of a distribution. Let’s say the random variable of our interest is X then, moments are defined as the X’s expected values.

For Example, E(X), E(X²), E(X³), E(X⁴),…, etc.

Use of Moment in Statistics

  • These are very useful in statistics because they tell you much about your data.
  • The four commonly used moments in statistics are- the mean, variance, skewness, and kurtosis.

To be ready to compare different data sets we will describe them using the primary four statistical moments.

The First Moment

  • The first central moment is the expected value, known also as an expectation, mathematical expectation, mean, or average.
  • It measures the location of the central point.

Case-1: When all outcomes have the same probability of occurrence

It is defined as the sum of all the values the variable can take times the probability of that
value occurring. Intuitively, we can understand this as the arithmetic mean.

Case-2: When all outcomes don’t have the same probability of occurrence

This is the more general equation that includes the probability of each outcome and is defined as the summation of all the variables multiplied by the corresponding probability.

Conclusion

For equally probable events, the expected value is exactly the same as the Arithmetic Mean. This is one of the most popular measures of central tendency, which we also called Averages. But, there are some other common measures also like, Median and Mode.

  • Median — The middle value
  • Mode — The most likely value.

The Second Moment

  • The second central moment is “Variance”.
  • It measures the spread of values in the distribution OR how far from the normal.
  • Variance represents how a set of data points are spread out around their mean value.

For Example, for a sample dataset, you can find the variance as mentioned below:

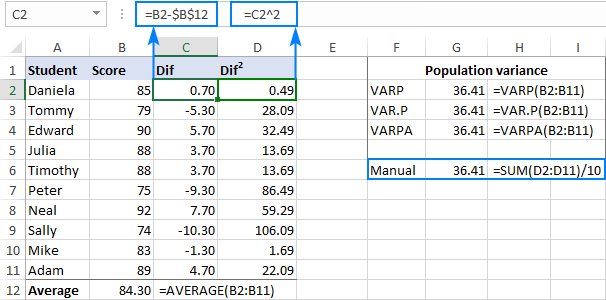
How to calculate variance in Excel – sample & population variance formula - Ablebits.com

Standard Deviation

Standard deviation is just a square root of the variance and is commonly used since the unit
of random variable X and Standard deviation is the same, so interpretation is easier.

For Example, For a normal distribution:

moments in Statistics
  • 1 st Standard Deviation: 68.27% of the data points lie
  • 2 nd Standard Deviation: 95.45% of the data points lie
  • 3 rd Standard Deviation: 99.73% of the data points lie

Now. let’s understand the answer to the given questions:

Why Variance is preferred over Mean Absolute Deviation(MAD)?

Variance is preferred over MAD due to the following reasons:

Mathematical properties: The function of variance in both Continuous and differentiable.

For a Population, the Standard Deviation of a sample is a more consistent estimate: If we picked the repeated samples from a normally distributed population, then the standard deviations of samples are less spread out as compared to mean
absolute deviations.

The Third Moment

  • The third statistical moment is “Skewness”.
  • It measures how asymmetric the distribution is about its mean.

We can differentiate three types of distribution with respect to its skewness:

Symmetrical Distribution

If both tails of a distribution are symmetrical, and the skewness is equal to zero, then that distribution is symmetrical.

Positively Skewed

In these types of distributions, the right tail (with larger values) is longer. So, this also tells us about ‘outliers’ that have values higher than the mean. Sometimes, this is also referred to as:

  • Right-skewed
  • Right-tailed
  • Skewed to the Right

Negatively Skewed

In these types of distributions, the left tail (with small values) is longer. So, this also tells us about ‘outliers’ that have values lower than the mean. Sometimes, this is also referred to as:

  • Left-skewed
  • Left-tailed
  • Skewed to the Left
moments in Statistics

For Example, For a Normal Distribution, which is Symmetric, the value of Skewness equals 0 and that distribution is symmetrical.

In general, Skewness will impact the relationship of mean, median, and mode in the  described manner:

  • For a Symmetrical distribution: Mean = Median = Mode
  • For a positively skewed distribution: Mode < Median < Mean (large tail of high values)
  • For a negatively skewed distribution: Mean < Median < Mode (large tail of small values)

But the above generalization is not true for all possible distributions.

For Example, if one tail is long, but the other is heavy, this may not work. The best way to explore your data is to first compute all three estimators and then try to draw conclusions based on the results, rather than just focusing on the general rules.

Other Formula of Calculating Skewness

Skewness = (Mean-Mode)/SD = 3*(Mean-Median)/SD

Since, (Mode = 3*Median-2*Mean)

Some transformations to make the distribution normal:

For Positively skewed (right): Square root, log, inverse, etc.

For Negatively skewed (left): Reflect and square[sqrt(constant-x)], reflect and log, reflect
and inverse, etc.

The Fourth Moment

  • The fourth statistical moment is “kurtosis”.
  • It measures the amount in the tails and outliers.
  • It focuses on the tails of the distribution and explains whether the distribution is flat or rather with a high peak. This measure informs us whether our distribution is richer in extreme values than the normal distribution.

For Example, For a normal distribution, the value of Kurtosis equals 3

For Kurtosis not equal to 3, there are the following cases:

  • Kurtosis<3 [Lighter tails]: Negative kurtosis indicates a broad flat distribution.
  • Kurtosis>3 [Heavier tails]: Positive kurtosis indicates a thin pointed distribution.

In general, we can differentiate three types of distributions based on the Kurtosis:

Mesokurtic

These types of distributions are having the kurtosis of 3 or excess kurtosis of 0. This category includes the normal distribution and some specific binomial distributions.

Leptokurtic

These types of distributions are having a kurtosis greater than 3, or excess kurtosis greater than 0. This is the distribution with fatter tails and a more narrow peak.

Platykurtic

These types of distributions are having the kurtosis smaller than 3 or excess kurtosis less than 0(negative). This is a distribution with very thin tails compared to the normal distribution.

Now, let’s define what is Excess Kurtosis

Excess Kurtosis = Kurtosis – 3

Understanding of Kurtosis related to Outliers:

  • Kurtosis is defined as the average of the standardized data raised to the fourth power. Any standardized values less than |1| (i.e. data within one standard deviation of the mean) will contribute petty to kurtosis.
  • The standardized values that will contribute immensely are the outliers.
  • Therefore, the high value of Kurtosis alerts about the presence of outliers.

Different Types of Moments

Let’s discuss three different types of moments:

Raw Moments

The raw moment or the n-th moment about zero of a probability density function f(x) is the expected value of X^n. It is also known as the Crude moment.

Centered Moments

A central moment is a moment of a probability distribution of a random variable defined about the mean of the random variable’s i.e, it is the expected value of a specified integer power of the deviation of the random variable from the mean.

Standardized Moments

A standardized moment of a probability distribution is a moment that is normally a higher degree central moment, but it is normalized typically by dividing the standard deviation which renders the moment scale-invariant.

Python Code Examples to Calculate Moments

Here are some examples to calculate moments in statistics:

First Moment (Mean)

import numpy as np

data = [10, 12, 15, 20, 25]

mean = np.mean(data)
print("Mean:", mean)

Output

Mean: 16.4

Second Moment (Variance)

import numpy as np

data = [10, 12, 15, 20, 25]

variance = np.var(data)
print("Variance:", variance)

Output

Variance: 29.839999999999996

Third Moment (Skewness)

import numpy as np
from scipy.stats import skew

data = [10, 12, 15, 20, 25]

skewness = skew(data)
print("Skewness:", skewness)

Output

Skewness: 0.4081372552079214

Fourth Moment (Kurtosis)

import numpy as np
from scipy.stats import kurtosis

data = [10, 12, 15, 20, 25]

kurt = kurtosis(data)
print("Kurtosis:", kurt)

Output

Kurtosis: -1.2717442086121507

End Note

Moments in statistics are an essential statistical concept that every data scientist should know. They provide valuable insights into data distribution and help understand its central tendency, spread, and shape. By understanding moments, data scientists can make informed data analysis and modeling decisions. Whether calculating the mean and variance or exploring higher-order moments, a solid grasp of moments is crucial for accurately interpreting and manipulating data. Incorporating moments into your data science toolkit will enhance your ability to extract meaningful information and derive valuable insights from datasets. Embrace the power of moments and elevate your data science skills to new heights. You can read the following articles to learn other essential statistics functions:

Frequently Asked Questions

Q1. What is the formula for moment in statistics?

A. The formula for the moment in statistics depends on the order of the moment. For example, the first moment (mean) formula is Σ(xi)/n, where xi is each value in the dataset and n is the number of data points.

Q2. What are moments in probability?

A. Moments in probability theory are mathematical quantities used to describe the shape and characteristics of probability distributions. They provide insights into random variables’ behavior and help quantify properties like central tendency and dispersion.

Q3. Why are moments in statistics called moments?

A. Moments in statistics are called moments because they capture a distribution’s “essence” or “character.” The term “moment” comes from Latin, meaning “movement” or “force.” Moments capture the movement or tendency of data points away from a reference point (such as the mean) and provide information about the distribution’s shape and properties.

Q4. What is the 5th moment in statistics?

A. The 5th moment in statistics refers to the fifth-order moment, which provides information about the shape and asymmetry of a distribution. It quantifies the distribution’s departure from symmetry and can indicate the presence of heavy tails or skewness.

The media shown in this article is not owned by Analytics Vidhya and are used at the Author’s discretion.

Chirag Goyal
Chirag Goyal

I am a B.Tech. student (Computer Science major) currently in the pre-final year of my undergrad. My interest lies in the field of Data Science and Machine Learning. I have been pursuing this interest and am eager to work more in these directions. I feel proud to share that I am one of the best students in my class who has a desire to learn many new things in my field.

Free Courses

Generative AI 4.7

Generative AI - A Way of Life

Explore Generative AI for beginners: create text and images, use top AI tools, learn practical skills, and ethics.
Large Language Models 4.5

Getting Started with Large Language Models

Master Large Language Models (LLMs) with this course, offering clear guidance in NLP and model training made simple.
Prompt Engineering 4.6

Building LLM Applications using Prompt Engineering

This free course guides you on building LLM apps, mastering prompt engineering, and developing chatbots with enterprise data.
LlamaIndex 4.8

Improving Real World RAG Systems: Key Challenges & Practical Solutions

Explore practical solutions, advanced retrieval strategies, and agentic RAG systems to improve context, relevance, and accuracy in AI-driven applications.
RAG systems using LlamaIndex 4.7

Microsoft Excel: Formulas & Functions

Master MS Excel for data analysis with key formulas, functions, and LookUp tools in this comprehensive course.

Recommended Articles

Responses From Readers

Clear

Write for us

Write, captivate, and earn accolades and rewards for your work
  • Reach a Global Audience
  • Get Expert Feedback
  • Build Your Brand & Audience
  • Cash In on Your Knowledge
  • Join a Thriving Community
  • Level Up Your Data Science Game
imag

We use cookies essential for this site to function well. Please click to help us improve its usefulness with additional cookies. Learn about our use of cookies in our Privacy Policy & Cookies Policy.

Show details